Plane stress ve Plane strain, sonlu elemanlar analizi yazılımlarında "mesh" ayarları kısmında eleman özelliklerini belirlerken karşımıza çıkan, elastisite teorisi ve sürekli cisimler mekaniği derslerinden birini alanların kesinlikle isimlerini duyduğu, ikileme gibi birinin ismini anarken diğerini de çoğunlukla andığımız iki kardeş kavramdır. Peki plane stress ve plane strain nedir, nerelerde kullanılır, arkasında yatan teori nedir ?
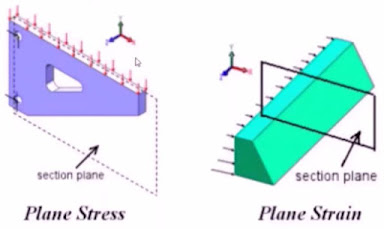
Sürekli cisimler mekaniği, bir malzemenin herhangi bir P noktasındaki gerilmeyi, asal gerilmelerinden sadece biri "0" ise "plane stress" hali olarak adlandırır. Bu durumda gerilme tensörü 3x3 lük matristen 2x2 lik bir matrise indirgenir ve çözüm kolaylaşır. Aslında asıl amaç da budur, çözümü basitleştirmek. Plane stress aslında bir varsayımdır ve plane stress halinden bahsedebilmek için yüklemenin "in-plane" bir yükleme olması gerekir.
Plane stress, in-plane yüke maruz kalan ince cidarlı yapılarda kullanılmak için uygundur. Çünkü kalınlık boyunca kesitte oluşan "out of plane stress" göz ardı edilebilir. İnce bir plakayı ısıttığımızı düşünelim, plaka genleşmek isteyecek ve uzayacaktır. Poisson oranına bağlı olarak kesit kalınlığı da incelmek isteyecektir ve bunu engelleyen bir durum ortada yoktur, yani parça herhangi bir yerinden kısıtlanmamıştır. Kalınlık yönündeki deformasyonu engellemediğimiz için gerilme de görmeyiz. Bu durum "plane stress" halidir.
Plane stress, yüzey boyunca herhangi bir noktasında yüke maruz kalmayan kalın parçaların yüzey kısımlarında da uygulanır. Hatta bu durum tam bir plane stress halidir çünkü direkt olarak yüzey söz konusudur ve ihmal edilen bir kalınlık söz konusu değildir.
Plane stress, ince cidarlı basınçlı kapların analizlerinde de sıkça kullanılır çünkü ince cidardan dolayı radyal gerilme ihmal edecek kadar azdır ve sıfır kabul edilir.
Sürekli cisimler mekaniği, bir malzemenin herhangi bir P noktasındaki gerinmeyi, asal gerinmelerinden sadece biri "0" ise "plane strain" hali olarak adlandırır. Aynı şekilde, gerinme tensörü 3x3 lük matristen 2x2 lik bir matrise indirgenir ve çözüm kolaylaşır. Amaç yine çözümü basitleştirmektir. Plane strain aslında bir varsayımdır ve plane strain halinden bahsedebilmek için yüklemenin "in-plane" bir yükleme olması gerekir.Bir boyut, diğer iki boyuta göre oldukça büyük ise, plane strain yaklaşımı uygulanır ve büyük boyutun olduğu yöndeki gerinme kısıtlanır. Yani cismin boyutu o yönde o kadar büyüktür ki orada oluşacak gerinme "0" kabul edilecek kadar küçüktür.
Bir çubuğu ele alalım, çubuğun iki ucunu da sabitleyelim. Çubuğu ısıttığımızda çubuk uzamak isteyecek fakat sabitlediğimiz için uzayamayacak. Out of plane yönünde termal gerinme sabit mesnetler tarafından kısıtlanacak fakat bununla beraber gerilme oluşacaktır. Bu durum "plane strain" halidir.
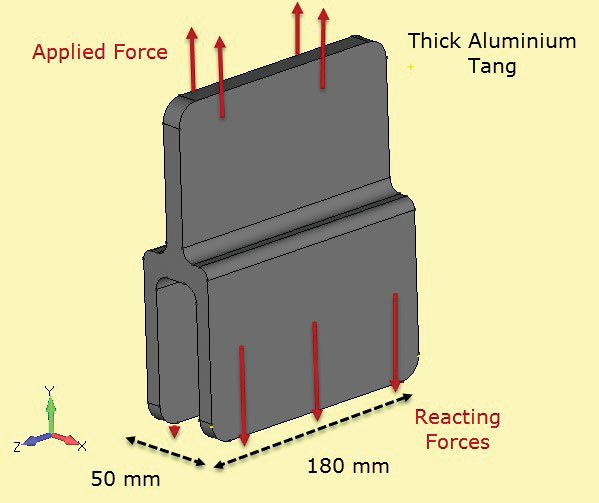
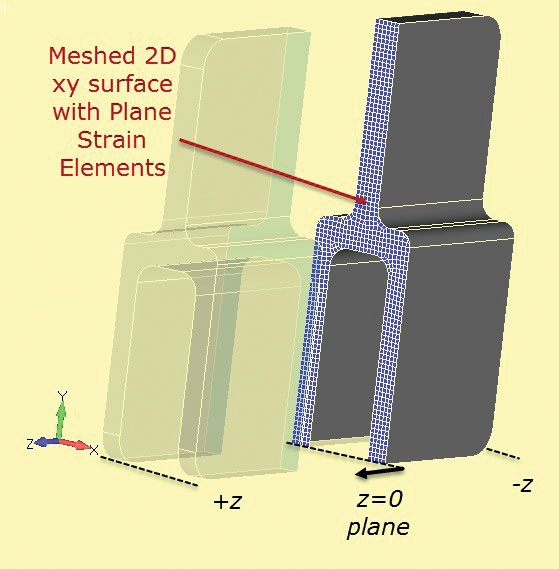
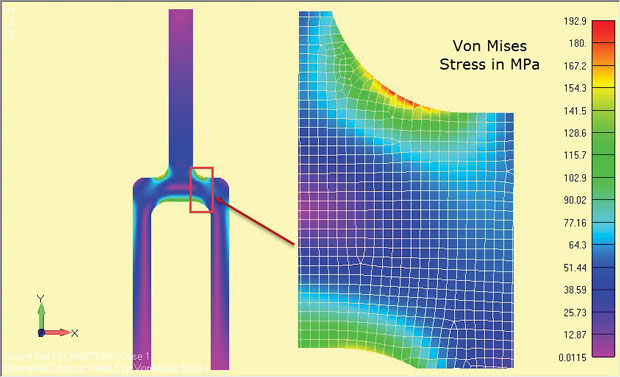
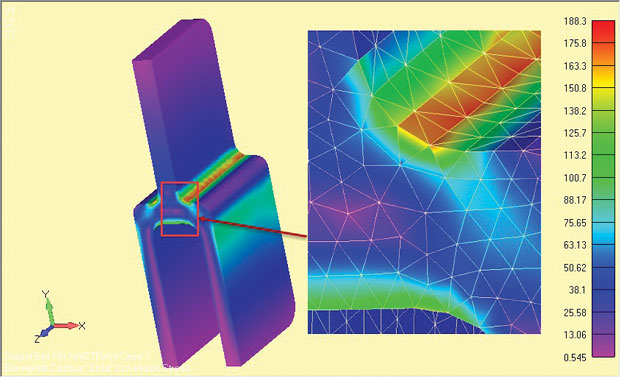
Aşağıdaki resimlerde z yönünde epey kalın bir alüminyum parça, sadece in plane yükleme altında ve geometrinin kesiti "plane strain" elemanlar ile meshleniyor. Von-Mises eşdeğer gerilme sonuçları birbirine çok yakın. Plane strain varsayımı ile çok daha sıkı bir ağ yapısı örerek çok daha kısa zamanda bir analiz yapılmış.3 boyutlu analiz sonucunda maksimum değerin çok az düşük çıkmasının sebebi 2 boyutlu meshe göre daha kaba şekilde ve tetrahedron elemanlarla meshlenmesidir.
https://www.fidelisfea.com/post/plane-stress-vs-plane-strain-what-are-they-and-which-should-you-chooseSchaum's Outline of Continuum Mechanics
https://en.wikipedia.org/wiki/Plane_stress
https://sites.engineering.ucsb.edu/~hpscicom/projects/stress/introge.pdf
https://www.digitalengineering247.com/article/simplifying-fea-models-plane-stress-and-plane-strain/fea
https://www.quora.com/Solid-Mechanics-What-are-the-differences-between-plane-stress-and-plane-strain-conditions
https://www.youtube.com/watch?v=78K0pbvHzjM
*Öğrendiklerimi unutmamak ve bildiğim kadarıyla paylaşmak adına bu bloğu oluşturdum, yanlış bilgi gördüğünüz takdirde yorumlarda belirtirseniz sevinirim.
*Bilgi, paylaştıkça çoğalır.







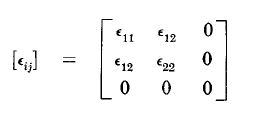
Yorumlar
Yorum Gönder